Tri par insertion
Présentation
Le tri par insertion est un autre algorithme que l’on peut qualifier de naïf. Cet algorithme consiste à piocher une à une les valeurs du tableau et à les insérer, au bon endroit, dans le tableau trié constitué des valeurs précédemment piochées et triées. Les valeurs sont piochées dans l’ordre où elles apparaissent dans le tableau. Soit p l’indice de la valeur piochée, les (p-1) premières valeurs du tableau constituent le tableau trié dans lequel va être inséré la pième valeur. Au début de l’algorithme, il faut considérer que la liste constituée du seul premier élément est trié : c’est vrai puisque cette liste ne comporte qu’un seul élément. Ensuite, on insère le second élément (p=2), puis le troisième (p=3) etc. Ainsi, p varie de 2 à n, où n est le nombre total d’éléments du tableau.
Le problème de cet algorithme est qu’il faut parcourir le tableau trié pour savoir à quel endroit insérer le nouvel élément, puis décaler d’une case toutes les valeurs supérieures à l’élément à insérer. En pratique, le tableau classé est parcouru de droite à gauche, c’est à dire dans l’ordre décroissant. Les éléments sont donc décalés vers la droite tant que l’élément à insérer est plus petit qu’eux.. Dés que l’élément à insérer est plus grand qu’un des éléments du tableau triée il n’y a plus de décalage, et l’élément est inséré dans la case laissée vacante par les éléments qui ont été décalés.
Exemple
Grandes étapes de l’évolution du tableau au fil de l’algorithme. En bleu, le tableau trié, en rouge, la valeur de la mémoire qui contient la valeur à insérer.
| Tableau | Memoire | |||||
| 5 | 3 | 1 | 2 | 6 | 4 | 3 |
| 3 | 5 | 1 | 2 | 6 | 4 | 1 |
| 1 | 3 | 5 | 2 | 6 | 4 | 2 |
| 1 | 2 | 3 | 5 | 6 | 4 | 6 |
| 1 | 2 | 3 | 5 | 6 | 4 | 4 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Pseudo langage | |||||||
| C / C++ | Caml | Java | OCaml | ||||
Complexité
Soit un tableau de n éléments, pour mettre en œuvre le tri par insertion, il faut insérer un à un (n-1) éléments dans un tableau préalablement trié. Dans le pire des cas, c’est à dire quand la liste à trier de manière croissante est classée de manière décroissante, pour insérer le pième élément, il faut décaler les (p-1) éléments qui le précédent. Soit une complexité totale, dans le pire des cas, donnée par la formule suivante :
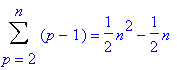
Cependant, en moyenne, seul la moitié des éléments est décalée. Soit un décalage de (p-1)/2 éléments et donc une complexité en moyenne qui se calcule ainsi :
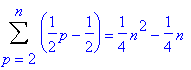
Là encore, il s’agit d’une complexité en O(n2) analogue à la complexité du tri bulle optimisé et du tri par sélection. Cependant, le tri par insertion présente un avantage certain : il peut être facilement mis en oeuvre pour insérer de nouvelles données dans un tableau déjà trié ou pour trier des valeurs au fur et à mesure de leur apparition (cas des algorithmes en temps réel ou il faut parfois exploiter une série de valeurs triées qui viens s’enrichir, au fil du temps, de nouvelles valeurs). C’est l’un des seuls tri dont la complexité est meilleure quand le tableau initial posséde un "certain ordre".
![]() Accueil des algorithmes de tri
Accueil des algorithmes de tri
![]() Article précédent : le tri par sélection
Article précédent : le tri par sélection
![]() Article suivant : le tri Shell
Article suivant : le tri Shell
